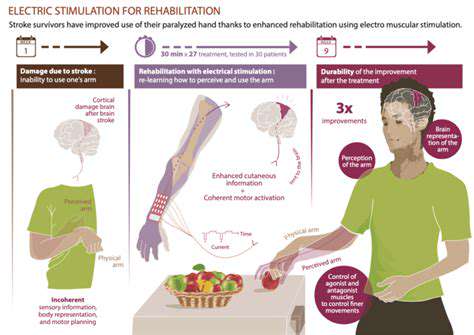
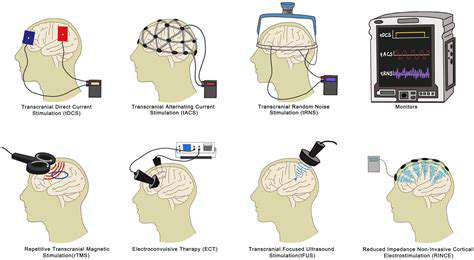
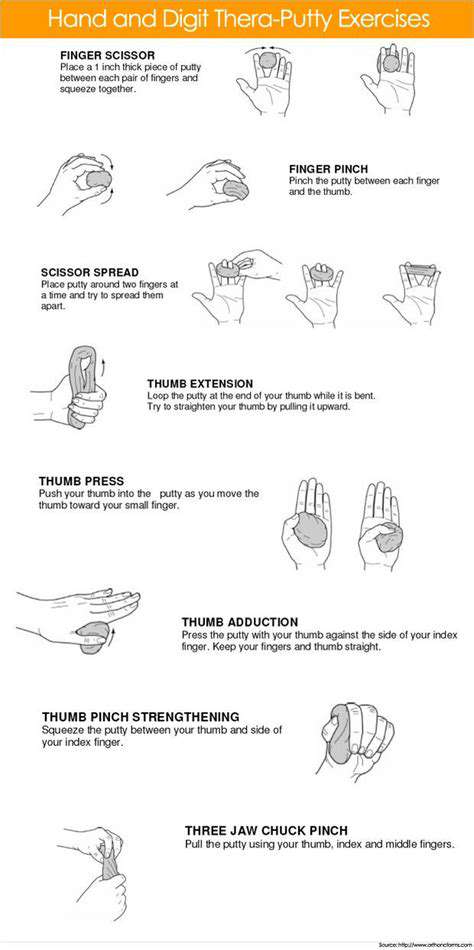
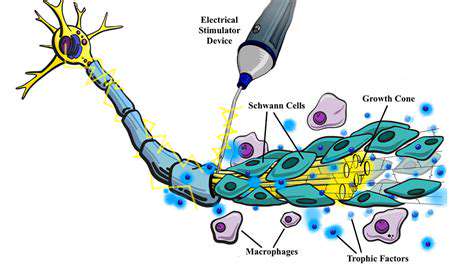
Premier Approaches to Finger Coordination and Control

Music Composition and Performance

Music composition utilizes mathematical principles in rhythm, harmony, and melody, shaping soundscapes that evoke emotion and tell stories. Analyzing the mathematical structures within various musical styles, from classical sonatas to modern electronic music, reveals patterns and relationships that enhance our understanding of musical expression and creativity. This interdisciplinary approach fosters a deeper appreciation for the art form and its underlying mathematical foundations.

Beyond composition, the application of mathematical principles extends to musical performance. Precision timing and rhythmic accuracy are crucial in ensemble playing and solo performances. Understanding mathematical concepts like fractions and ratios allows musicians to effectively interpret scores and maintain a consistent tempo, leading to a more cohesive and engaging performance experience. The interplay between music and mathematics is evident in the meticulous practice and dedication required to master a musical instrument or to perform complex compositions.

Sports Performance Enhancement

Sports performance is significantly influenced by mathematical principles. Analyzing data like speed, trajectory, and reaction time, often using sophisticated statistical methods, helps athletes optimize their training and performance. For example, understanding projectile motion allows athletes like baseball players and archers to maximize the distance and accuracy of their throws or hits. The principles of physics are deeply intertwined with sports performance, enabling athletes to enhance their techniques and achieve peak performance.

Furthermore, mathematical models can be used to predict outcomes and analyze strategies in various sports. For instance, in team sports, mathematical analyses of player positions and team formations can help optimize team strategies and predict game outcomes. This data-driven approach allows coaches to make informed decisions, leading to improved team performance and a better understanding of the dynamics of the game.

Engineering Design and Problem Solving

Engineering design heavily relies on mathematical principles to solve complex problems and create innovative solutions. From calculating structural loads to optimizing energy efficiency, mathematical models and equations are fundamental tools in the engineering process. The ability to apply these principles accurately and effectively is crucial for creating functional and safe structures, machines, and systems. The use of mathematical tools allows engineers to translate abstract ideas into tangible, real-world applications.

In addition to design, mathematics is essential for problem-solving in engineering. Whether it's troubleshooting a faulty machine or developing a new technology, mathematical modeling and analysis help engineers understand the underlying issues and develop effective solutions. The use of mathematical tools and techniques fosters a systematic and logical approach to problem-solving, leading to innovative and effective solutions.

Financial Modeling and Investment Strategies

Financial modeling plays a crucial role in the world of finance, using mathematical models and statistical analysis to predict market trends, assess investment opportunities, and manage risk. These models allow investors to analyze large amounts of data, identify patterns, and make informed decisions about portfolio allocation and investment strategies. Mathematical principles are essential for understanding market dynamics and mitigating potential risks.

Furthermore, mathematical models are employed in various financial instruments and asset pricing. By understanding and applying mathematical concepts, financial professionals can design and evaluate investment strategies, assess the potential returns and risks associated with different investments, and optimize portfolio performance. This allows for better decision-making in the financial world and contributes to the overall stability and growth of the market.

Medicine and Healthcare Applications

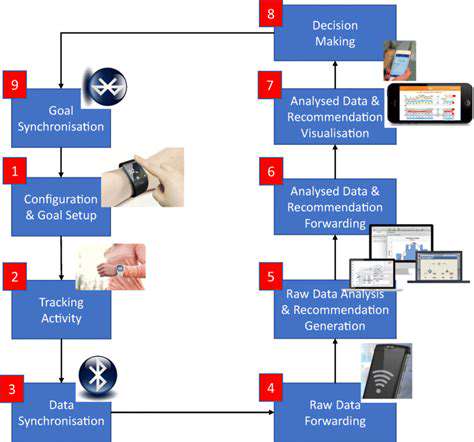
The field of medicine increasingly utilizes mathematical models to improve diagnoses, treatments, and patient outcomes. Mathematical modeling can assist in drug development, personalized medicine, and disease prediction. Using mathematical tools, researchers can analyze complex biological systems, simulate drug interactions, and predict disease progression. The application of mathematical principles allows for a more precise and targeted approach to healthcare.

Mathematical modeling also helps in medical imaging and diagnostics. Techniques like CT scans and MRIs rely on mathematical algorithms to create detailed images of internal structures. These techniques allow doctors to visualize and analyze complex anatomical features, aiding in the diagnosis and treatment of various medical conditions. The use of mathematical tools in healthcare fosters a more accurate and effective approach to medical practice.